3535.
Вася и матрица
Вася получил от
мамы в подарок прямоугольную матрицу размером n × m. В каждой ячейке этой матрицы записано
целое число. Сначала Вася с увлечением играл в различные математические игры с
матрицей: то стремительно вычислял её детерминант, то с лёгкостью возводил её в
разные степени.
Однако вскоре
такие игры ему наскучили, и он придумал себе новое развлечение: Вася выбирает
целое число k и пытается найти подматрицу
максимальной площади, сумма всех элементов которой не превышает k. Подматрицей
называется прямоугольный фрагмент исходной матрицы.
Вход. В первой строке заданы три целых
числа: n, m и k (1 ≤ n, m ≤ 300, 1
≤ k ≤ 109).
Далее
следуют n строк, в каждой из которых записано по m неотрицательных
целых чисел, каждое из которых не превышает 1000.
Выход. Выведите одно число – площадь
наибольшей подматрицы, сумма элементов в которой не превосходит k.
|
Пример
входа |
Пример
выхода |
|
3 3 12 7 5 7 8 4 8 4 3 2 |
3 |
РЕШЕНИЕ
динамическое программирование + бинарный поиск
Анализ алгоритма
Пусть a –
входная прямоугольная матрица. Создадим двумерный массив dp такого же размера,
где dp[i][j] – это сумма элементов в подматрице с противоположными вершинами в точках (1, 1) и (i, j).
Значения в
этом массиве можно вычислить по следующей формуле:
dp[i][j]
= dp[i – 1][j] + dp[i][j – 1] – dp[i – 1][j – 1] + a[i][j]
Рассмотрим
подматрицу массива a размером w
* h. Пусть ее противоположные углы находятся в точках с
координатами (i, j) и (i + w – 1, j + h
– 1).
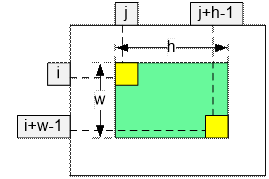
Тогда сумма всех чисел в
подматрице вычисляется по формуле:
dp[i + w
– 1][j + h – 1] – dp[i + w – 1][j – 1] – dp[i – 1][j + h
– 1] + dp[i – 1][j – 1]
Решаем задачу
полным перебором. Перебираем все возможные размеры подматрицы w × h,
а также все допустимые координаты левого верхнего угла (i, j)
этой подматрицы. С помощью массива dp за постоянное время определяем
сумму чисел внутри текущей подматрицы. Если эта сумма не превышает k, то
среди всех таких подматриц запоминаем максимальную площадь.
Однако такой
перебор работает за O(n4),
что слишком долго. Мы можем ускорить его до O(n3logn) с
помощью бинарного поиска по ширине h подматрицы.
Зафиксируем
левый верхний угол (i, j). Обозначим через g(w, h)
сумму
элементов подматрицы с вершинами (i,
j) и (i + w – 1, j + h
– 1). Если зафиксировать высоту w, а
ширину h рассматривать как
переменную, то функция g(w, h) будет неубывающей по h, так
как исходная матрица a содержит неотрицательные целые числа. Это
позволяет применять бинарный поиск для нахождения максимального значения h, при котором g(w, h)
≤ k.
Пример
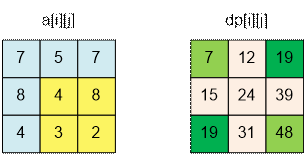
Например, сумма
чисел в
подматрице с углами в точках (2, 2) и (3, 3) равна
48 – 19 – 19 + 7
= 17
Реализация
алгоритма
Входную матрицу
храним в массиве а.
#define MAX 210
int a[MAX][MAX], dp[MAX][MAX];
Функция f(w, h) возвращает 1, если существует подматрица
размера w × h, сумма элементов в которой не превышает k.
Для этого перебираются все возможные координаты левого верхнего угла (i, j), и с помощью массива dp
за константное время вычисляется сумма элементов в прямоугольнике с вершинами (i, j)
и (i + w
– 1, j + h – 1).
int f(int w, int h)
{
for (int i = 1; i + w
- 1 <= n; i ++)
for (int j = 1; j + h
- 1 <= m; j ++)
if (dp[i + w - 1][j + h - 1] - dp[i + w
- 1][j - 1] –
dp[i - 1][j + h - 1] + dp[i - 1][j - 1] <= k) return 1;
return 0;
};
Основная часть программы. Читаем входную матрицу.
scanf("%d
%d %d",&n,&m,&k);
for
(i = 1; i <= n; i++)
for
(j = 1; j <= m; j++)
scanf("%d",&a[i][j]);
На основе входной матрицы a вычисляем вспомогательную матрицу dp.
for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + a[i][j];
Перебираем возможные значения ширины подматрицы w.
answer = 0;
for (w = 1; w <= n; w++)
{
Длину подматрицы перебираем с помощью бинарного поиска на отрезке
[l; r].
l = 1; r = m;
while (l < r)
{
mid =
(l + r) / 2;
Для подматрицы размером w * mid перебираем все возможные позиции её
левого верхнего угла (i, j). Если существует хотя бы одно положение, при котором сумма
элементов в подматрице не превышает k, обновляем значение
результирующей площади answer.
if (f(w,mid))
{
answer = max(answer, w * mid);
l =
mid + 1;
}
else r = mid;
}
mid =
(l + r) / 2;
if (f(w,mid))
answer = max(answer, w * mid);
};
Выводим площадь найденной максимальной
подматрицы.
printf("%d\n",answer);